空讲大道理，就是忽悠。我们还是从题目说起：

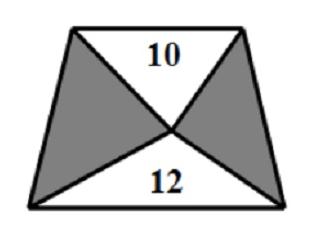
　　如图，在一个梯形内有两个面积分别为10与12 的三角形，已知梯形的上底长是下底长的2/3，那么余下阴影部分的面积是？。

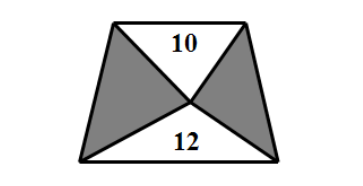
　　这是96年奥数赛的真题。

　　一种解法是按照比例关系来解题。我们知道上下两个三角形面积的比（5:6），也知道梯形上下底的比（2:3），就可以计算出上下两个三角形高的比，并进一步算出梯形的高和其中一个三角形高的比。根据这些比例关系就可以计算出梯形面积和这个三角形面积的比。再用梯形面积减去两个三角形的面积，就是阴影部分的面积。这是一种算术的解法。

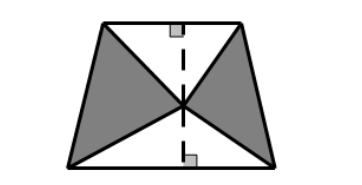
　　但是这一题如果用几何的解法来做，要有趣的多。这就要灵活运用到关于三角形、梯形、平行四边形的知识。

　　如果我们从两个三角形公共的顶点，做一条平行于梯形上下底的平行线。只要三角形的公共顶点在这条平行线上，那么三角形的面积不变。

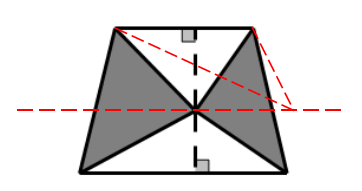
　　比如我们把这个顶点移到平行线和梯形的一条边的交点，如下图，上下两个三角形的面积仍然分别是10和12，而阴影部分变成了一个三角形，面积不变。

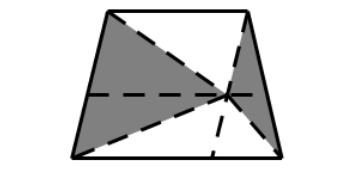
　　虽然我们把阴影部分变成了一个三角形，但是这个三角形的面积并不好算。所以我们要考虑在这个图形上再做一些变化。

　　现在，我们还有一个条件没有用到，也就是梯形上下底的长度比。

　　我们从梯形上底的一个顶点出发，做一条平行于梯形另外一边的平行线，如下图，这样我们把梯形分割成了一个平行四边形和三角形。然后我们把两个三角形的公共顶点移到这两条线相交的位置。

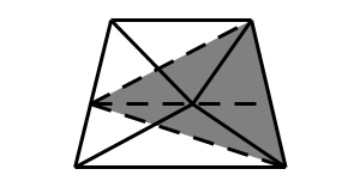
　　因为我们是在平行线上移动三角形的顶点，所以三角形的面积不变。上面的三角形面积等于10。而下面的三角形被分割成了两个小三角形，因为梯形上底和下底的长度比为2:3，所以这两个小三角形底边长的比为2：1，面积分别是8和4。

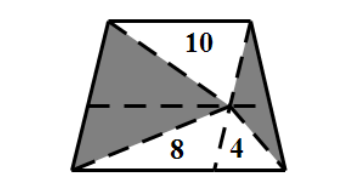
　　最后，我们来算梯形的面积。

　　左边的平行四边形的面积是平行四边形内两个三角形面积的两倍，也就是（10＋8）×2=36。右边的三角形和平行四边形的高相等，底是平行四边形的一半，所以三角形的面积等于36÷2÷2=9。梯形的面积等于36+9=45，阴影部分的面积等于45－10－12=23。

　　我们在学习三角形、梯形这样的基本图形时，老师都会用一种又直观又漂亮的推导方法来讲解面积的算法。即，用割补的方法，从矩形到平行四边形，再从平行四边形到三角形和梯形。

　　等到学完之后，老师会让我们记住一个个公式，像什么底乘以高除以二。公式化记忆对于应付考试当然是最高效的，但是对学数学来说还不够。

　　如果我们遇到一个问题，公式没法用或者不好用怎么办？这就需要我们理解公式，而不光是记住公式。这道题就是一个例子。

　　所以，家长让小孩去学奥数，应该首先立足于为数学学习打下更扎实的基础，适量的做一些这样的练习，就一定会有收获。

　　这个系列，到这期就结束了，要看前面几期，可以点这里：一、二、三、四

　　更多数学学习的文章，请关注微信公众号【怎样学数学】。微信搜索【howtolearnmath】，即可关注。